先備知識

量子狀態的表達通常是用Bra–ket notation，下面這是ket notation表示法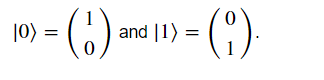

量子基本態如下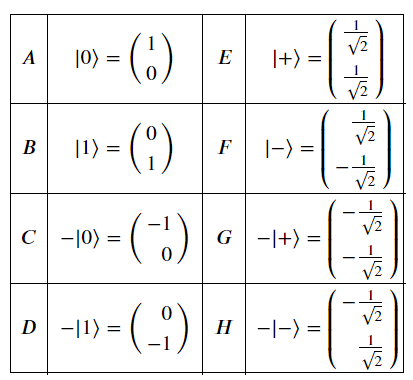

而量子的疊加態表示法如下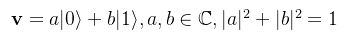

下面則是用qiskit套件實現一個基本的疊加態

# import all necessary objects and methods for quantum circuits
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer

# define a quantum register with one qubit
q =  QuantumRegister(1,"qreg")

# define a classical register with one bit
# it stores the measurement result of the quantum part
c = ClassicalRegister(1,"creg")

# define our quantum circuit
qc = QuantumCircuit(q,c)

# apply h-gate (Hadamard: quantum coin-flipping) to the first qubit
qc.h(q[0])

# measure the first qubit, and store the result in the first classical bit
qc.measure(q,c)

# draw the circuit by using matplotlib
qc.draw(output='mpl') # re-run the cell if the figure is not displayed

1.引入套件後
2.創建一個bit的量子暫存器儲存量子位
3.同時建立一個經典暫存器用於接收量子態測量後的資訊
4.之後就是把量子暫存器與經典暫存器結合成一個量子電路
5.並施加一個Hadamard Gate
6.最後就是將量子態的測量結果傳到經典暫存器
7.將量子電路圖畫出
輸出結果如下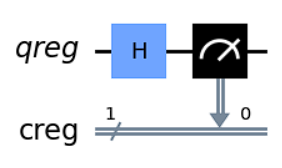

Hadamard Gate就是主要用於將基本量子態轉換成疊加態的Operator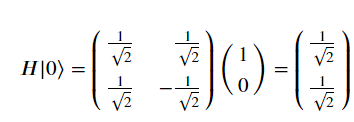

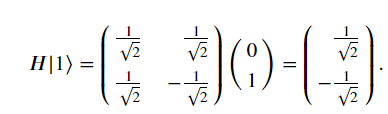
實際模擬

前面的程式碼只是用來架構量子電路而已，還無法模擬量子態，接下來就是要用電腦去實際模擬量子操作後的結果

# execute the circuit 10000 times in the local simulator
job = execute(qc,Aer.get_backend('qasm_simulator'),shots=10000)
counts = job.result().get_counts(qc)
print(counts) # print the outcomes

print()
n_zeros = counts['0']
n_ones = counts['1']
print("State 0 is observed with frequency %",100*n_zeros/(n_zeros+n_ones))
print("State 1 is observed with frequency %",100*n_ones/(n_zeros+n_ones))

# we can show the result by using histogram
print()
from qiskit.visualization import plot_histogram
plot_histogram(counts)

輸出結果:

{'0': 5116, '1': 4884}
State 0 is observed with frequency % 51.16
State 1 is observed with frequency % 48.84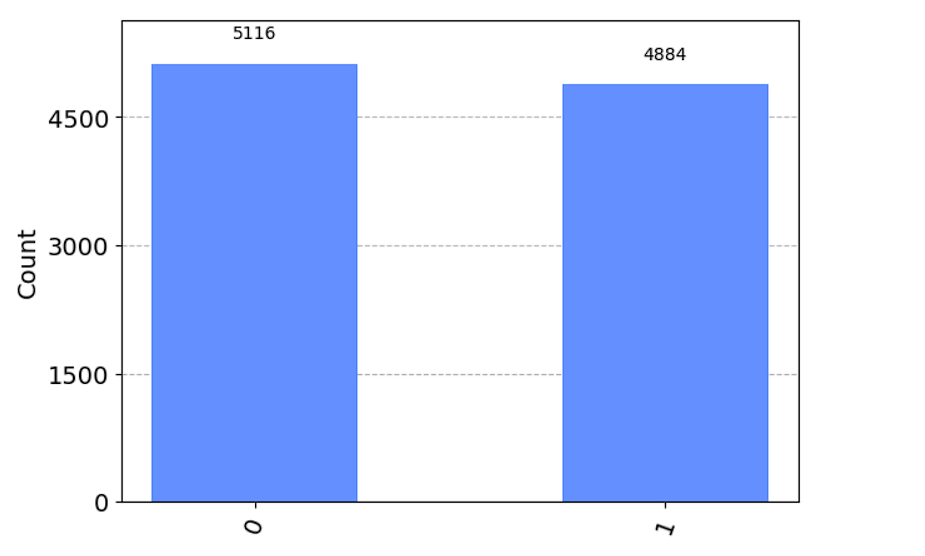

從結果可以看到，Hadamard Gate可以將量子態疊加至約略0.5|0>+0.5|1>
之所以不是完美的50% 50%是因為實際量子電路的操作會有雜訊，並不完美

若想疊加至其他機率狀態可以用Rotation matrix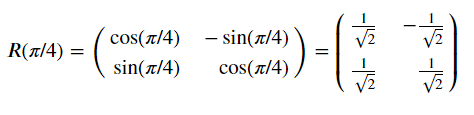

Qiskit實作如下

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram
from math import pi

# we define a quantum circuit with one qubit and one bit
q =  QuantumRegister(1) # quantum register with a single qubit
c = ClassicalRegister(1) # classical register with a single bit
qc = QuantumCircuit(q,c) # quantum circuit with quantum and classical registers

# angle of rotation in radian
rotation_angle = 2*pi/3

# rotate the qubit with rotation_angle
qc.ry(2*rotation_angle,q[0]) 

# measure the qubit
qc.measure(q,c)

# draw the circuit
qc.draw(output='mpl')

輸出電路圖

電腦模擬

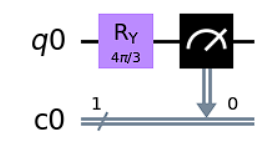
# execute the program 1000 times
job = execute(qc,Aer.get_backend('qasm_simulator'),shots=1000)

# print the results
counts = job.result().get_counts(qc)
print(counts)

# draw the histogram
plot_histogram(counts)

輸出結果

{'1': 750, '0': 250}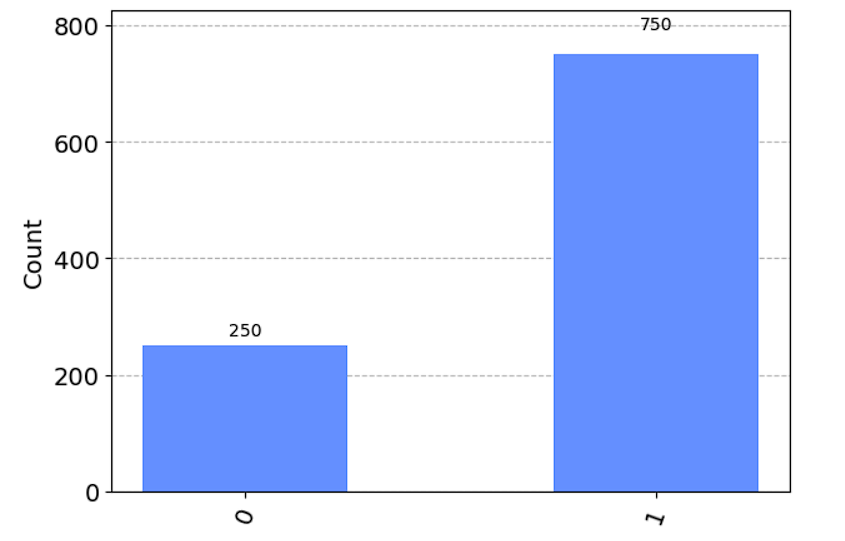

參考資料：Qworld教材